开创性的数学公式为健康能源和食品行业的激动人心的进步铺平了道路

一个突破性的数学方程可以在未来改变医疗程序、天然气开采和塑料包装生产。由布里斯托大学的科学家开发的新方程表明，通过可渗透材料的扩散运动首次可以精确建模。它是在世界领先的物理学家阿尔伯特·爱因斯坦和玛丽安·冯·斯莫鲁霍夫斯基推导出第一个扩散方程一个世纪之后，标志着从微观粒子和自然有机体到人造设备的广泛实体的运动表示方面取得了重要进展。

到目前为止，科学家通过多孔材料(例如生物组织、聚合物、各种岩石和海绵)观察粒子运动，不得不依赖近似或不完整的视角。

今天发表在《物理评论研究》杂志上的研究结果提供了一种新技术，可以在包括健康、能源和食品工业在内的各种环境中提供令人兴奋的机会。

主要作者TobyKay，正在完成博士学位。工程数学博士说：“这标志着自爱因斯坦和斯莫鲁霍夫斯基对扩散的研究以来向前迈出了根本性的一步。它通过从细胞成分和地质化合物到环境栖息地的所有尺度的复杂介质，彻底改变了扩散实体的建模。

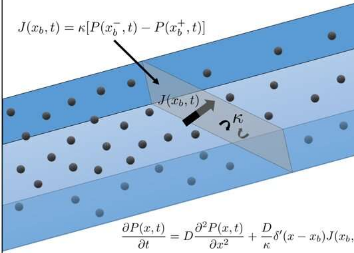
“以前，通过散布有阻碍运动的物体(称为渗透障碍)的环境来表示运动的数学尝试受到限制。通过解决这个问题，我们正在为许多不同领域的激动人心的进步铺平道路，因为渗透障碍经常遇到动物、细胞生物和人类。”

数学中的创造力有不同的形式，其中之一是对现象的不同描述层次之间的联系。在这种情况下，通过以微观方式表示随机运动，然后缩小以宏观描述该过程，就有可能找到新的方程。

需要进一步研究将这种数学工具应用于实验应用，从而改善产品和服务。例如，能够准确地模拟水分子通过生物组织的扩散将促进扩散加权MRI(磁共振成像)读数的解释。它还可以更准确地表示空气在食品包装材料中的传播，帮助确定保质期和污染风险。此外，量化觅食动物与栅栏和道路等宏观障碍相互作用的行为，可以更好地预测气候变化的后果，以实现保护目的。

在过去的20年中，地理定位器、移动电话和其他传感器的使用已经见证了跟踪革命产生了数量和质量不断增加的运动数据。这突出了对更复杂的建模工具的需求，以表示从自然生物到人造设备的广泛实体在其环境中的运动。

资深作者、布里斯托大学复杂性科学副教授LucaGiuggioli博士说：“这个新的基本方程是构建工具和技术来表示空间异质时扩散的重要性的另一个例子;也就是说，当底层环境因地点而异。

“它建立在2020年另一个期待已久的数学难题解决方案的基础上，以描述密闭空间中的随机运动。这一最新发现是在提高我们对各种形状和形式的运动的理解方面又向前迈出的重要一步——统称为数学运动——它有许多令人兴奋的潜在应用。”