从动态的角度进行深度学习

NUS 数学家开发了一个基于动态系统的新理论框架，以了解深度神经网络何时以及如何学习任意关系。尽管在实践中取得了广泛的成功，但理解深度学习的理论原理仍然是一项具有挑战性的任务。最基本的问题之一是：深度神经网络能否学习任意输入-输出关系(在数学中，这些被称为函数)，它们实现这一点的方式与传统方法有什么不同?

为了理解这个问题，有必要思考与传统的函数逼近范式相比，深度神经网络到底有什么新东西。例如，经典傅里叶级数将复杂函数近似为简单函数(例如正弦和余弦)的加权和。深度神经网络的运作方式完全不同。它们不是加权和，而是从简单函数(层)的重复堆叠中构建复杂函数。这在数学中也称为函数组合。关键问题是如何通过将简单的函数堆叠在一起来构建复杂的函数。事实证明，这是被称为近似理论的数学分支中的一个相当新的问题。

在这项发表在《欧洲数学会杂志》上的研究中，新加坡国立大学数学系李倩晓助理教授及其合作者开发了一种新的函数组合逼近能力理论。一个有趣的观察是，虽然函数组合由于其离散和非线性结构而在实践中难以分析，但这并不是第一次出现此类问题。

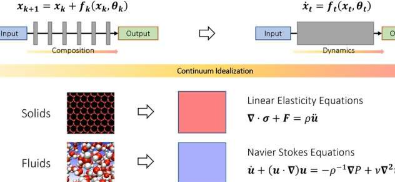
在研究固体和流体的运动时，常常将它们理想化为粒子的连续体，满足一些连续方程(常微分方程或偏微分方程)。这可以避免在离散的原子级别上对此类系统进行建模的困难。相反，导出了在宏观水平上模拟它们的行为的连续方程。

该研究的关键思想是，通过将分层结构理想化为连续动态系统，该概念可以扩展到深度神经网络。这将深度学习与称为动力系统的数学分支联系起来。这种联系允许开发新工具来理解深度学习的数学，包括对何时确实可以近似任意关系的一般表征。

李教授说：“深度学习的动力系统观点提供了一个有前途的数学框架，它突出了深度神经网络与传统范式相比的不同方面。这带来了动力系统、逼近理论和机器学习接口上令人兴奋的新数学问题。 "

“未来发展的一个有希望的领域是扩展这个框架以研究深度神经网络的其他方面，例如如何有效地训练它们以及如何确保它们在看不见的数据集上更好地工作，”李教授补充道。

　　免责声明：本文由用户上传，与本网站立场无关。财经信息仅供读者参考，并不构成投资建议。投资者据此操作，风险自担。 如有侵权请联系删除！