病毒式数学方程式难倒互联网的简单原因

大约十年来，数学家和数学教育工作者一直在权衡一场根植于学校数学的特定辩论，这场辩论没有减弱的迹象。Slate、 Popular Mechanics、《纽约时报》和许多其他媒体都报道了这场辩论，焦点集中在一个如此“病毒式”传播的方程式上，以至于它最终与其他“破坏”或“分裂”的现象混为一谈。互联网。

如果你还没有权衡，现在是看看你的立场的好时机。请回答以下问题：

8÷2(2+2)=?

如果您像大多数人一样，您的答案是 16 并且惊讶于其他人可以找到不同的答案。除非，也就是说，你和大多数其他人一样，你的答案是 1，而你同样对以另一种方式看待它感到困惑。不要害怕，在下文中，我们将解释这个问题的明确答案——以及为什么应该禁止写公式的方式。

我们的兴趣之所以被激发，是因为我们对遵循运算顺序(面对数学方程式时采取的一系列步骤)的惯例进行了研究，并且对所有大惊小怪的内容感到有些困惑。

显然，答案是……

一个数学问题的两个可行答案?好吧，如果我们都记得数学课上的一件事：那是不对的!

许多主题来自解释这个“方程式”如何以及为何打破互联网的大量文章。在计算器上输入表达式，其中一些被编程为尊重特定的操作顺序，引起了很多讨论。

其他人，对冲了一下，建议两个答案都是正确的(这很荒谬)。

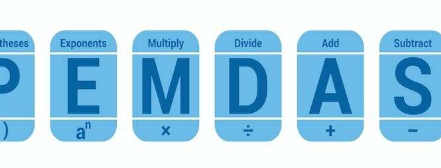
最主要的主题只是专注于根据不同的首字母缩写词执行操作顺序。一些评论员表示，人们的误解归咎于对不同国家所教的记住操作顺序的首字母缩写词的错误解释，例如美国有时使用的 PEMDAS：PEMDAS 是指应用括号、指数、乘法、除法、加法和减法。

由于以括号开头，遵循此顺序的人将 8÷2(2+2) 变为 8÷2(4)。那么 8÷2(4) 就变成了 8÷8 因为没有指数，而“M”代表乘法，所以他们将 2 乘以 4。最后，根据除法的“D”，他们得到 8÷8= 1.

相比之下，加拿大人可能会被教导记住 BEDMAS，它代表应用括号、指数、除法、乘法、加法和减法。由于以括号开头(与括号相同)，遵循此顺序的人会将 8÷2(2+2) 变为 8÷2(4)。然后，8÷2(4) 变为 4(4)，因为(没有指数)并且“D”代表除法。最后，根据乘法的“M”，4(4)=16。

如果问题正确地表述为 8 ÷ 2 × (2 + 2) = ?，就不会有激烈的争论。学分：Egan J. Chernoff，作者提供

不要省略乘号

对我们来说，表达式 8÷2(2+2) 在语法上是错误的。

我们认为，争论的关键在于括号前的乘法符号被省略了。

这种省略是代数中的惯例。例如，在代数中，我们写成 2x 或 3a，这意味着 2 × x 或 3 × a。当字母用于变量或常量时，省略乘号。考虑著名的方程 e=mc 2，它表明能量的计算为 e=m×c 2。

那么，8÷2(2+2) 打破互联网的真正原因源于省略乘法符号的做法，这种做法不恰当地从代数引入到算术中。

不适当的优先级

换句话说，如果表达式被正确地“拼写”，即表示为“8 ÷ 2 × (2 + 2) = ?”，就不会有病毒式传播，没有二元性，没有破碎的互联网，没有激烈的辩论。没有什么好玩的!

最终，省略乘法符号会导致不适当的乘法优先级。所有评论员都同意在方括号或括号中添加条款是适当的第一步。但是考虑到 2 到 (4) 相对于 8 在 8÷2(4) 中的接近，出现了混淆。

我们想让它知道写 2(4) 来指代乘法是不合适的，但我们知道它一直在做，而且无处不在。

乘法的好符号

有一个非常好的乘法符号，所以让我们使用它：2 × 4。如果您不是粉丝，还有其他符号，例如 2•4。随意使用，但不要省略。

因此，郑重声明，关于 1 对 16 的辩论现在结束了!答案是 16。案件结案。此外，一开始就不应该有真正的辩论。